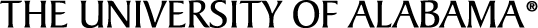|
Usually problems that carry more than one threat (double, triple, etc.) are considered to be flawed. However, if the threats are uniquely forced then interesting effects can happen. In the Fleck theme, the key makes multiple threats (3 or more) and the moves of Black force each of threats. The point is that the Fleck theme is a dual avoidance theme. In the pure form there should be no duals. The Fleck theme was named after Ferenc Fleck who created several examples in the mid 1900s. Interested readers please see David Shire's review of Ian Shanahan's collection of miniature ideal Fleck. We begin with one such problem.
1 Comment
seetharaman kalyan
12/27/2020 03:38:52 am
Nice article. Parthasarathi composed the ultimate fleck zagoriko! I don't recollect the position.
Reply
Leave a Reply. |
Chess ProblemsOn the side I like to dabble in chess problem composition. I am mostly interested in two and three move direct mates. I hope to convey the beauty and logic of chess problems with this blog. In the entries are some of my favorite problems and my own problems. Before looking at the problems I suggest reading this introduction to the chess problem world by the British Chess Problem Society. Also, here is a list of terminology and themes. Here is a link to my problems on yacpdb. ARTICLES
1. "Choose wisely" The Problemist Supplement, Sept. 2016 2. "Double checking white in a two mover" StrateGems July 2016 3. "Double check without capture" The Problemist Supplement, January 2018 4. "The disappearing Nowotny: Part I" The Problemist Supplement, March 2018 5. "The disappearing Nowotny: Part II" The Problemist Supplement, May 2018 6. "The disappearing Nowotny: Part III" The Problemist Supplement, July 2018 7. "Castling with half-battery and Fleck themes" StrateGems, July 2018 8. "The Baku Nowotny" StrateGems, January 2019 9. "The Romanian Nowotny with Fleck" The Problemist, March 2019 10. "Mirror Image" The Problemist Supplement, May 2019 11. "White King in Check" Problemas, July 2019 12. "A Simple Mechanism", StrateGems, July 2019 13. "Miniatures with castling and (partial) Fleck" Problemist Supplement, September 2019 14. "Taking the Straitjacket off the Fleck" The Problemist Supplement, November 2019 15. "Unforced threats" The Problemist Supplement, May 2020 16. "Ojanen in Miniature" The Problemist Supplement, May 2020 17. "Developments in the Finnish Nowotny" The Problemist, July 2020 18. "Categorising the Fleck theme" The Problemist, January 2021 19. "Masking the Bristol" The Problemist Supplement, March 2021 20. "My love of the Novotny" StrateGems July 2021 21. "Masked Novotny" The Problemist Supplement, November 2021 Archives
August 2022
Categories |

 RSS Feed
RSS Feed